In the figure, DE || QR and AP and BP

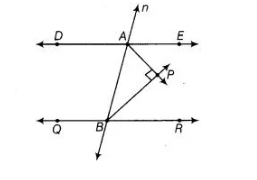
Given, $D E \| Q R$ and $A P$ and $P B$ are the bisectors of $\angle E A B$ and $\angle R B A$, respectively.

We know that, the interior angles on the same side of transversal are supplementary.

$\therefore$   $\angle E A B+\angle R B A=180^{\circ}$

$\Rightarrow \quad \frac{1}{2} \angle E A B+\frac{1}{2} \angle R B A=\frac{180^{\circ}}{2} \quad$ [dividing both sides by 2]

$\Rightarrow \quad \frac{1}{2} \angle E A B+\frac{1}{2} \angle R B A=90^{\circ}$ ...(i)

Since, $A P$ and $B P$ are the bisectors of $\angle E A B$ and $\angle R B A$, respectively.

$\therefore$ $\angle B A P=\frac{1}{2} \angle E A B$ .....(ii)

and $\angle A B P=\frac{1}{2} \angle R B A$ ...(iii)

On adding Eqs. (ii) and (iii), we get

$\angle B A P+\angle A B P=\frac{1}{2} \angle E A B+\frac{1}{2} \angle R B A$

From Eq. (i),

$\Rightarrow \quad \angle B A P+\angle A B P=90^{\circ}$ ..(iv)

In $\triangle A P B, \quad \angle B A P+\angle A B P+\angle A P B=180^{\circ}$ [sum of all angles of a triangle is $180^{\circ}$ ]

$\Rightarrow \quad 90^{\circ}+\angle A P B=180^{\circ}$ [from Eq. (iv)]

$\Rightarrow \quad \angle A P B=180^{\circ}-90^{\circ}=90^{\circ}$