Question:
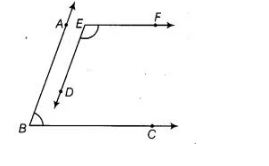
In the figure, BA || ED and BC || EF. Show that ∠ABC + ∠DEF = 180°.
Solution:
Given BA || ED and BC || EF
To show, ∠ABC + ∠DEF = 180°
Construction Draw a ray PE opposite to ray EF.
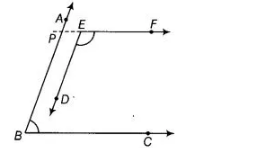
Proof in the figure, $B C \| E F$
$\therefore \angle E P B+\angle P B C=180^{\circ}$ [sum of cointerior angles is $180^{\circ}$ ] ...(i)
Now, $A B \| E D$ and $P E$ is a transversal line.
$\therefore \quad \angle E P B=\angle D E F \quad$ [corresponding angles] ...(ii)
From Egs. (i) and (ii), $\quad \angle D E F+\angle P B C=180^{\circ}$
$\Rightarrow \quad \angle A B C+\angle D E F=180^{\circ}$ $[\because \angle P B C=\angle A B C]$
