In the figure, ABCD and EFGD are two parallelograms

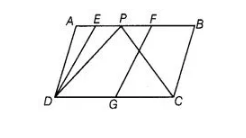
False

In the given figure, join PG. Since, G is the mid-point of CD.

Thus, PG is a median of ΔDPC and it divides the triangle into parts of equal areas.

Then, $\operatorname{ar}(\Delta D P G)=\operatorname{ar}(\Delta G P C)=\frac{1}{2} \operatorname{ar}(\Delta D P C)$ ...(i)

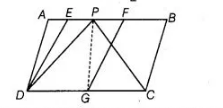
Also, we know that, if a parallelogram and a triangle lie on the same base and between the same parallels, then area of triangle is equal to half of the area of parallelogram.

Here, parallelogram EFGD and $\triangle D P G$ lie on the same base $D G$ and between the same paraliels $D G$ and $E F$.

So, $\operatorname{ar}(\Delta D P G)=\frac{1}{2} \operatorname{ar}(E F G D)$ ...(ii)

From Eqs. (i) and (ii), $\frac{1}{2} \operatorname{ar}(\Delta D P C)=\frac{1}{2} \operatorname{ar}(E F G D)$

$\Rightarrow$ $\operatorname{ar}(\triangle D P C)=\operatorname{ar}(E F G D)$