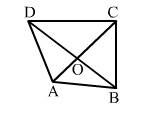
In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.

Given:  BO = OD
To prove: ar(∆ABC) = ar(∆ADC)
Proof: 
Since BO = OD, O is the mid point of BD.
We know that a median of a triangle divides it into two triangles of equal areas.
CO is a median of ∆BCD.
i.e., ar(∆COD) = ar (∆COB)            ...(i)

AO is a median of ∆ABD.
i.e., ar(∆AOD) = ar(∆AOB)              ...(ii)

From (i) and (ii), we have:
ar(∆COD) + ar(∆AOD) = ar(∆COB) + ar(∆AOB)
∴ ar(∆ADC )​ = ar(∆ABC)