Question:
In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO = OD, prove that
ar(∆ABC) = ar(∆ADC),
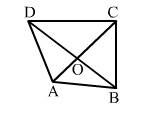
Solution:
Given: BO = OD
To prove: ar(∆ABC) = ar(∆ADC)
Proof:
Since BO = OD, O is the mid point of BD.
We know that a median of a triangle divides it into two triangles of equal areas.
CO is a median of ∆BCD.
i.e., ar(∆COD) = ar (∆COB) ...(i)
AO is a median of ∆ABD.
i.e., ar(∆AOD) = ar(∆AOB) ...(ii)
From (i) and (ii), we have:
ar(∆COD) + ar(∆AOD) = ar(∆COB) + ar(∆AOB)
∴ ar(∆ADC ) = ar(∆ABC)
