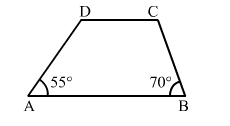
In the adjoining figure, ABCD is a trapezium in which AB || DC.

We have $A B \| D C$.

$\angle \mathrm{A}$ and $\angle \mathrm{D}$ are the interior angles on the same side of transversal line $\mathrm{AD}$, whereas $\angle \mathrm{B}$ and $\angle \mathrm{C}$ are the interior angles on the same side of transversal line $\mathrm{BC}$.

Now, $\angle \mathrm{A}+\angle \mathrm{D}=180^{\circ}$

$\Rightarrow \angle \mathrm{D}=180^{\circ}-\angle \mathrm{A}$ $\therefore \angle \mathrm{D}=180^{\circ}-55^{\circ}=125^{\circ}$

Again, $\angle \mathrm{B}+\angle \mathrm{C}=180^{\circ}$

$\Rightarrow \angle \mathrm{C}=180^{\circ}-\angle \mathrm{B}$

$\therefore \angle \mathrm{C}=180^{\circ}-70^{\circ}=110^{\circ}$