In the adjoining figure, ABC is a triangle in which AB = AC.

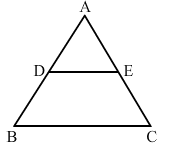
Given:
AD = AE     ...(i)
AB = AC     ...(ii)
Subtracting AD from both sides, we get:
⇒">⇒⇒ AB -">−- AD = AC -">−- AD
⇒">⇒⇒ AB -">−- AD = AC -">−- AE  (Since, AD = AE)
⇒">⇒⇒BD = EC    ...(iii)
Dividing  equation  (i) by equation (iii), we get:

$\frac{A D}{D B}=\frac{A E}{E C}$

Applying the converse of Thales' theorem, $D E \| B C$

$\Rightarrow \angle D E C+\angle E C B=180^{\circ}$ (Sum of interior angles on the same side of a transversal line is $180^{\circ} .$ )

$\Rightarrow \angle D E C+\angle C B D=180^{\circ}$ (Since, $A B=A C \Rightarrow \angle B=\angle C$ )

Hence, quadrilateral BCED is cyclic.

Therefore, B,C,E and D are concyclic points.