Question:
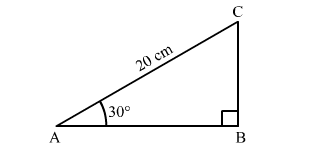
In the adjoining figure, $\triangle A B C$ is a right-angled triangle in which $\angle B=90^{\circ}, \angle A=30^{\circ}$ and $A C=20 \mathrm{~cm}$.
Find
(i) BC,
(ii) AB.
Solution:
From the given right-angled triangle, we have:
$\frac{B C}{A C}=\sin 30^{\circ}$
$\Rightarrow \frac{B C}{20}=\frac{1}{2}$
$\Rightarrow B C=\frac{20}{2}=10 \mathrm{~cm}$
Also, $\frac{A B}{A C}=\cos 30^{\circ}$
$\Rightarrow \frac{A B}{20}=\frac{\sqrt{3}}{2}$
$\Rightarrow A B=\left(20 \times \frac{\sqrt{3}}{2}\right)=10 \sqrt{3} \mathrm{~cm}$
$\therefore \mathrm{BC}=10 \mathrm{~cm}$ and $\mathrm{AB}=10 \sqrt{3} \mathrm{~cm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.