In the adjoining figure
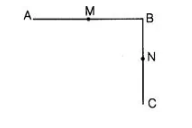
(i) $A B=B C, M$ is the mid-point of $A B$ and $N$ is the mid-point of $B C$. Show that $A M=N C$.
(ii) $B M=B N, M$ is the mid-point of $A B$ and $N$ is the mid-point of $B C$. Show that $A B=B C$.
(i) Given,$A B=B C$ $\ldots$ (i)
$M$ is the mid-point of $A B$.
$\therefore$ $A M=M B=\frac{1}{2} A B$ ...(ii)
and $N$ is the mid-point of $B C$.
$\therefore$ $B N=N C=\frac{1}{2} B C$ ....(iii)
According to Euclid's axiom, things which are halves of the same things are equal to one another.
From Eq. (i), $A B=B C$
On multiplying both sides by $\frac{1}{2}$, we get
$\frac{1}{2} A B=\frac{1}{2} B C$
$\Rightarrow$ $A M=N C$ [using Eqs. (ii) and (iii)]
(ii) Given, $B M=B N$ $\ldots$ (i)
$M$ is the mid-point of $A B$.
$\therefore$$A M=B M=\frac{1}{2} A B$
$\Rightarrow$ $2 A M=2 B M=A B$... (ii)
and $N$ is the mid-point of $B C$.
$\therefore$ $B N=N C=\frac{1}{2} B C$
$\Rightarrow$ $2 B N=2 N C=B C$ ...(iii)
According to Euclid's axiom, things which are double of the same thing are equal to one another.
On multiplying both sides of Eq. (i) by 2, we get
$2 B M=2 B N$
$\Rightarrow$ $A B=B C$[using Eqs. (ii) and (iii)]
