In the accompanying diagram a fair spinner is placed at the centre O of the circle Diameter AOB and radius OC divide the circle into three regions labelled X, Y and Z. It ∠BOC = 45°. What is the probability that the spinner will land in the region X? (in the given figure).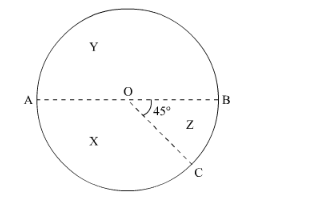
Given: A fair spinner is placed at the centre O of the circle. Diameter AOB and radius OC divide the circle into three regions labeled X, Y and Z and angle ![]()
To find: Probability that the spinner will land in X region?
Total angle of circle is 360°.
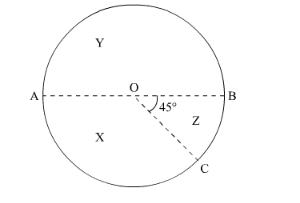
$\angle \mathrm{AOC}+\angle \mathrm{BOC}=180^{\circ}$ (Straight angle)
$\angle \mathrm{AOC}+45^{\circ}=180^{\circ}$
$\angle \mathrm{AOC}=180^{\circ}-45^{\circ}$
$\angle \mathrm{AOC}=135^{\circ}$..............(1)
We know that PROBABILITY $=\frac{\text { Number of favourable event }}{\text { Total number of event }}$
Hence probability of "spinner will land in $X$ region" is $\frac{135}{360}=\frac{3}{8}$
