Question:
In given figure $l \| m$ and $M$ is the mid-point of a line segment $A B$. Show that $M$ is also the mid-point of any line segment $C D$, having its end points on $I$ and $m$, respectively.
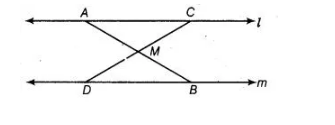
Solution:
Given In the figure, $l \| m$ and $M$ is the mid-point of a line segment $A B$ i.e., $A M=B M$.
To show $M C=M D .$
Proof $\because$ $l \| m$ [given]
$\angle B A C=\angle A B D$ [alternate interior angles]
$\angle A M C=\angle B M D$ [vertically opposite angles]
In $\triangle A M C$ and $\triangle B M D$, $\angle B A C=\angle A B D$ [proved above]
$A M=B M$ [given]
and $\angle A M C=\angle B M D$ [proved above]
$\therefore$ $\triangle A M C \cong \triangle B M D$ [by ASA congruence rule)
$\Rightarrow$ $M C=M D$ [by CPCT]
