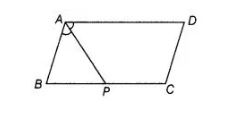
In figure, P is the mid-point of side

Given in a parallelogram $A B C D, P$ is a mid-point of $B C$ such that $\angle B A P=\angle D A P$.

To prove $A D=2 C D$

Proof Since, $A B C D$ is a parallelogram.

So, $A D \| B C$ and $A B$ is transversal, then

$\angle A+\angle B=180^{\circ}$  [sum of cointerior angles is $180^{\circ}$ ]

$\Rightarrow \quad \angle B=180^{\circ}-\angle A$ ...(i)

$\begin{array}{lll}\text { In } \triangle A B P_{1} & \angle P A B+\angle B+\angle B P A=180^{\circ} & \text { [by angle sum property of a triangle] }\end{array}$

In $\triangle A B P$, $\angle P A B+\angle B+\angle B P A=180^{\circ}$ [by angle sum property of a triangle]

$\Rightarrow \quad \frac{1}{2} \angle A+180^{\circ}-\angle A+\angle B P A=180^{\circ}$ [from Eq. (i)]

$\Rightarrow$ $\angle B P A-\frac{\angle A}{2}=0$

$\Rightarrow$ $\angle B P A=\frac{\angle A}{2}$ ...(ii)

$\Rightarrow$ $\angle B P A=\angle B A P$ 

$\Rightarrow$ $A B=B P$ [opposite sides of equal angles are equal]

On multiplying both sides by 2, we get

$2 A B=2 B P$

$\Rightarrow$ $2 A B=B C$ [since $P$ is the mid-point of $B C$ ]

$\Rightarrow$ $2 C D=A D$

[since, $A B C D$ is a parallelogram, then $A B=C D$ and $B C=A D$ ]