In figure, O is the centre of the circle,

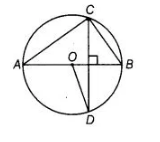
Given, in the figure $B D=O D, C D \perp A B$.

$\ln \triangle O B D$ $B D=O D$  [given]

$O D=O B$ [both are the radius of circle]

$\therefore$ $O B=O D=B D$

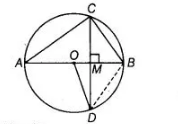
Thus, $\triangle O D B$ is an equilateral triangle.

$\therefore \quad \angle B O D=\angle O B D=\angle O D B=60^{\circ}$

In $\triangle M B C$ and $\triangle M B D$, $M B=M B$ [common side]

$\angle C M B=\angle B M D=90^{\circ}$

and $C M=M D$

[in a circle, any perpendicular drawn on a chord also bisects the chord]

$\therefore$  $\triangle M B C \cong \triangle M B D$ [by SAS congruence rule)

$\therefore$ $\angle M B C=\angle M B D$ [by CPCT]

$\Rightarrow$ $\angle M B C=\angle O B D=60^{\circ}$ $\left[\because \angle O B D=60^{\circ}\right]$

Since, $A B$ is a diameter of the circle.

$\therefore \quad \angle A C B=90^{\circ}$

$\begin{array}{ll}\text { In } \triangle A C B, & \angle C A B+\angle C B A+\angle A C B=180^{\circ}\end{array}$

[by angle sum property of a triangle]

$\Rightarrow \quad \angle C A B+60^{\circ}+90^{\circ}=180^{\circ}$

$\Rightarrow \quad \angle C A B=180^{\circ}-\left(60^{\circ}+90^{\circ}\right)=30^{\circ}$