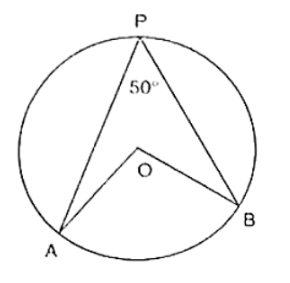
Question:
In figure, O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.
Solution:
∠APB = 50°
By degree measure theorem
∠AOB = 2∠APB
⇒ ∠APB = 2 × 50° = 100° since OA = OB [Radius of circle]
Then ∠OAB = ∠OBA [Angles opposite toequalsides]
Let ∠OAB = x
In ΔOAB, by angle sum property
∠OAB + ∠OBA + ∠AOB = 180°
⟹ x + x + 100° = 180°
⟹ 2x = 180° - 100°
⟹ 2x = 80°
⟹ x = 40°
∠OAB = ∠OBA = 40°
