In figure, if parallelogram $\mathrm{ABCD}$ and rectangle $\mathrm{ABEM}$ are of equal area, then
(a) perimeter of ABCD = perimeter of ABEM
(b) perimeter of ABCD < perimeter of ABEM
(c) perimeter of ABCD > perimeter of ABEM
(d) perimeter of ABCD = ½ (perimeter of ABEM)
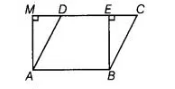
(c) In rectangle ABEM, AB = EM [sides of rectangle] and in parallelogram ABCD, CD = AB
On adding, both equations, we get
AB + CD = EM + AB …(i)
We know that, the perpendicular distance between two parallel sides of a parallelogram is always less than the length of the other parallel sides.
BE < BC and AM < AD
[since, in a right angled triangle, the hypotenuse is greater than the other side]
On adding both above inequalities, we get
SE + AM
On adding AB + CD both sides, we get
AB + CD + BC + AD> AB + CD + BE + AM
=> AB+BC + CD + AD> AB+BE + EM+ AM [∴ CD = AB = EM]
Perimeter of parallelogram ABCD > perimeter of rectangle ABEM
