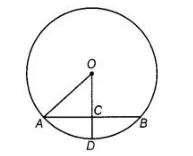
Question:
In figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to
(a) $2 \mathrm{~cm}$
(b) $3 \mathrm{~cm}$
(c) $4 \mathrm{~cm}$
(d) $5 \mathrm{~cm}$
Solution:
(a) We know that, the perpendicular from the centre of a circle to a chord bisects the chord.
AC = CB = ½ AB = ½ x 8 = 4 cm
given OA = 5 cm
AO2 = AC2 + OC2
(5)2 = (4)2 + OC2
25 = 16 + OC2
OC2 = 25-16 = 9
OC = 3 cm
[taking positive square root, because length is always positive]
OA = OD [same radius of a circle]
OD = 5 cm
CD = OD – OC = 5 – 3 = 2 cm
