Question:
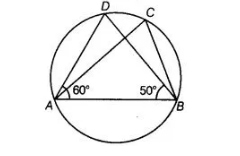
In figure, if $\angle D A B=60^{\circ}, \angle A B D=50^{\circ}$, then $\angle A C B$ is equal to
(a) 60°
(b) 50°
(c)70°
(d) 80°
Thinking Process
Use the theorem that angles in the same segment of a circle are equal and further simplify it.
Solution:
(c) Given, ∠DAB = 60°, ∠ABD = 50°
Since, ∠ADB = ∠ACB …(i)
[angles in same segment of a circle are equal]
In ΔABD, ∠ABD + ∠ADB + ∠DAB = 180° [by angle sum property of a triangle]
50°+ ∠ADB + 60° = 180°
=> ∠ADB = 180° – 110° = 70°
$\Rightarrow \angle \mathrm{ADB}=180^{\circ}-110^{\circ}=70^{\circ}$
