In figure, if AOB is a diameter

Solution:

(d) We know that, diameter subtends a right angle to the circle.

$\therefore \quad \angle B C A=90^{\circ}$ ....(i)

Given, $A C=B C$

$\Rightarrow$ $\angle A B C=\angle C A B$ ...(ii)

[angles opposite to equal sides are equal]

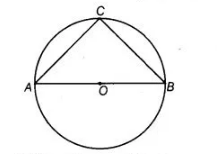
In $\triangle A B C$, $\quad \angle C A B+\angle A B C+\angle B C A=180^{\circ}$

[by angle sum property of a triangle]

$\Rightarrow \quad \angle C A B+\angle C A B+\angle 90^{\circ}=180^{\circ} \quad$ [from Eqs. (i) and (ii)]

$\Rightarrow \quad 2 \angle C A B=180^{\circ}-90^{\circ}$

$\Rightarrow \quad \angle C A B=\frac{90^{\circ}}{2}$

$\therefore \quad \angle C A B=45^{\circ}$