Question:
In figure, if ∠AOB = 90° and ∠ABC = 30°, then ∠CAO is equal to
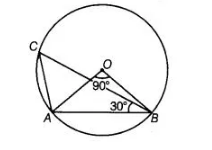
(a) 30°
(b) 45°
(c) 90°
(d) 60°
Solution:
(d)
In AOAB, ∠OAB + ∠ABO + ∠BOA = 180°
∠OAB + ∠OAB + 90° = 180° => 2∠OAB = 180°- 90°
[angles opposite to equal sides are equal] [angle sum property of a triangle] [from Eq. (i)]
=> ∠OAB = 90°/2 = 45° …(i)
In ΔACB, ∠ACB + ∠CBA + ∠CAB = 180°
∴ 45°+ 30°+ ∠CAB = 180°
=> ∠CAB = 180° – 75° = 105°
∠CAO+ ∠OAB = 105°
∠CAO + 45° = 105°
∠CAO = 105° – 45° = 60°
