Question:
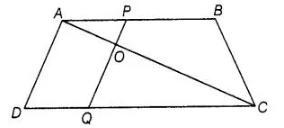
In figure, if AB || DC and AC, PQ intersect each other at the point 0. Prove that OA . CQ = 0C . AP.
Solution:
Given AC and PQ intersect each other at the point O and AB || DC
Prove that OA . CQ = 0C . AP
Proof $\ln \Delta A O P$ and $\Delta C O Q$, $\angle A O P=\angle C O Q \quad$ [vertically opposite angles]
$\angle A P O=\angle C Q O$
[since, $A B \| D C$ and $P Q$ is transversal, so alternate angles]
$\therefore \quad \Delta A O P \sim \Delta C O Q \quad$ [by AAA similarity criterion]
Then, $\frac{O A}{O C}=\frac{A P}{C Q}$ [since, corresponding sides are proportional]
$\Rightarrow$ $O A \cdot C Q=O C \cdot A P$ Hence proved.
