Question.
In figure, $\frac{Q R}{O S}=\frac{Q T}{P R}$ and $\angle 1=\angle 2$. Show that $\Delta P Q S \sim \Delta T Q R .$
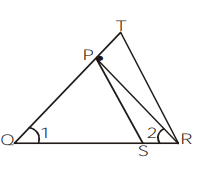
In figure, $\frac{Q R}{O S}=\frac{Q T}{P R}$ and $\angle 1=\angle 2$. Show that $\Delta P Q S \sim \Delta T Q R .$

Solution:
In figure, $\angle 1=\angle 2$ (Given)
$\Rightarrow \mathrm{PQ}=\mathrm{PR}$
(Sides opposite to equal angles of $\Delta \mathrm{PQR}$ )
We are given that
$\frac{Q R}{O S}=\frac{Q T}{P R}$
$\Rightarrow \frac{\mathrm{QR}}{\mathrm{OS}}=\frac{\mathrm{QT}}{\mathrm{PQ}} \quad(\because \mathrm{PQ}=\mathrm{PR}$ proved $)$
$\Rightarrow \frac{Q S}{Q R}=\frac{P Q}{Q T} \quad$ (Taking reciprocals) ...(1)
Now, in $\triangle \mathrm{PQS}$ and $\triangle \mathrm{TQR}$, we have
$\angle \mathrm{PQS}=\angle \mathrm{TQR} \quad($ Each $=\angle 1)$
and $\frac{\mathrm{OS}}{\mathrm{OR}}=\frac{\mathrm{PQ}}{\mathrm{OT}}$(By (1))
Therefore, by SAS similarity criterion, we have
$\Delta \mathrm{PQS} \sim \Delta \mathrm{TQR} .$
In figure, $\angle 1=\angle 2$ (Given)
$\Rightarrow \mathrm{PQ}=\mathrm{PR}$
(Sides opposite to equal angles of $\Delta \mathrm{PQR}$ )
We are given that
$\frac{Q R}{O S}=\frac{Q T}{P R}$
$\Rightarrow \frac{\mathrm{QR}}{\mathrm{OS}}=\frac{\mathrm{QT}}{\mathrm{PQ}} \quad(\because \mathrm{PQ}=\mathrm{PR}$ proved $)$
$\Rightarrow \frac{Q S}{Q R}=\frac{P Q}{Q T} \quad$ (Taking reciprocals) ...(1)
Now, in $\triangle \mathrm{PQS}$ and $\triangle \mathrm{TQR}$, we have
$\angle \mathrm{PQS}=\angle \mathrm{TQR} \quad($ Each $=\angle 1)$
and $\frac{\mathrm{OS}}{\mathrm{OR}}=\frac{\mathrm{PQ}}{\mathrm{OT}}$(By (1))
Therefore, by SAS similarity criterion, we have
$\Delta \mathrm{PQS} \sim \Delta \mathrm{TQR} .$
