Question.
In figure, $D E \| O Q$ and $D F \| O R$. Show that $E F \| Q R$.
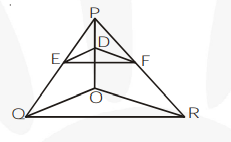
In figure, $D E \| O Q$ and $D F \| O R$. Show that $E F \| Q R$.
Solution:
In figure, $D E \| O Q$ and DF $\| O R$, then by Basic Proportionality Theorem,
We have $\quad \frac{P E}{E Q}=\frac{P D}{D O}....(1)
and $\quad \frac{P F}{F R}=\frac{P D}{D O}$\ldots(2)$
From $(1)$ and $(2), \quad \frac{P E}{E Q}=\frac{P F}{F R}$
Now, in $\triangle \mathrm{PQR}$, we have proved that
$\Rightarrow \frac{P E}{E Q}=\frac{P F}{F R}$
$\mathrm{EF} \| \mathrm{QR}$
(By converse of Basic Proportionality Theorem)
In figure, $D E \| O Q$ and DF $\| O R$, then by Basic Proportionality Theorem,
We have $\quad \frac{P E}{E Q}=\frac{P D}{D O}....(1)
and $\quad \frac{P F}{F R}=\frac{P D}{D O}$\ldots(2)$
From $(1)$ and $(2), \quad \frac{P E}{E Q}=\frac{P F}{F R}$
Now, in $\triangle \mathrm{PQR}$, we have proved that
$\Rightarrow \frac{P E}{E Q}=\frac{P F}{F R}$
$\mathrm{EF} \| \mathrm{QR}$
(By converse of Basic Proportionality Theorem)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.