In figure, D and E are points on side

Solution:

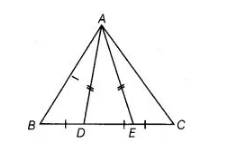
Given $D$ and $E$ are the points on side $B C$ of a $\triangle A B C$ such that $B D=C E$ and $A D=A E$.

To show $\triangle A B D \equiv \triangle A C E$

Proof We have, $A D=A E$ [given]

$\Rightarrow$ $\angle A D E=\angle A E D$ $\ldots(1)$

[since, angles opposite to equal sides are equal]

We have, $\angle A D B+\angle A D E=180^{\circ}$ [linear pair axiom]

$\Rightarrow$ $\angle A D B=180^{\circ}-\angle A D E$

$=180^{\circ}-\angle A E D$ [from Eq. (i)]

In $\triangle A B D$ and $\triangle A C E$, 

$\angle A D B=\angle A E C \quad\left[\because \angle A E C+\angle A E D=180^{\circ}\right.$, linear pair axiom $]$

$B D=C E$ [given]

and $A D=A E$ [given]

$\therefore$ $\triangle A B D \cong \triangle A C E$ [by SAS congruence rule]