Question:
In figure, CD||AE and CY||BA. Prove that ar (ΔCBX) = ar (ΔAXY).
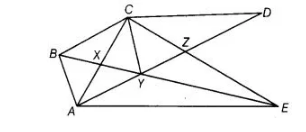
Solution:
Given In figure, CD||AE
and CY || BA
To prove ar (ΔCBX) = ar (ΔAXY) .
Proof We know that, triangles on the same base and between the same parallels are equal . in areas.
Here, ΔABY and ΔABC both lie on the same base AB and between the same parallels CY and BA.
ar (ΔABY) = ar (ΔABC)
=> ar (ABX) + ar (AXY) = ar (ABX) + ar (CBX)
=> ar (AXY) = ar (CBX) [eliminating ar (ABX) from both sides]
