Question:
In figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.
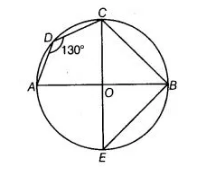
Solution:
We have, ∠ADC = 130° and chord BC – chord BE. Suppose, we consider the points A, B, C and D form a cyclic quadrilateral.
Since, the sum of opposite angles of a cyclic quadrilateral ΔDCB is 180°.
∠ADC + ∠OBC = 180°
=> 130°+ ∠OBC = 180°
=> ∠OBC = 180° -130° = 50°
In ΔBOC and ΔBOE,
BC = BE [given equal chord]
OC =OE [both are the radius of the circle]
and OB = OB [common side]
ΔBOC ≅ΔBOE
∠OBC = ∠OBE = 50° [by CPCT]
∠CBE = ∠CBO + ∠EBO = 50° + 50° = 100°
