In figure, ABCD is a trapezium in which AB || DC and DC = 40 cm and AB = 60 cm .If X and Y are, respectively,

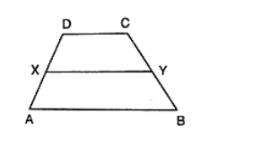
(i) Join DY and produce it to meet AB produced at P.

In triangles BYP and CYD we have,

∠BYP = ∠ CYD          [Vertically opposite angles]

∠DCY = ∠ PBY           [Since, DC ∥ AP]

And BY = CY

So, by ASA congruence criterion, we have

(ΔBYP) ≅ (ΔCYD)

⇒ DY = Yp and DC = BP

⇒ Y is the midpoint of DP

Also, x is the midpoint of AD

Therefore, XY ∥ AP and XY ∥ (1/2) AP

⇒ XY = (1/2) (AB + BP)

⇒ XY = (1/2) (AB + DC)

⇒ XY = (1/2) (60 + 40)

= 50 cm

(ii) We have, XY ∥ AP

⇒ XY ∥ AB and AB ∥ DC

⇒ XY ∥ DC

⇒ DCYX is a trapezium

(iii) Since x and y are the mid points of Ad and BC respectively.

Therefore, trapezium DCYX and ABYX are of the same height say h cm

Now,

ar(trap. DCXY) = (1/2)(DC + XY) × h

$\Rightarrow \operatorname{ar}(\operatorname{trap} . \mathrm{DCXY})=(1 / 2)(50+40) \times \mathrm{h} \mathrm{cm}^{2}=45 \mathrm{~h} \mathrm{~cm}^{2}$

⇒ ar(trap. ABYX) = (1/2)(AB + XY) × h

$\Rightarrow \operatorname{ar}(\operatorname{trap} \cdot A B Y X)=(1 / 2)(60+50) \times \mathrm{h} \mathrm{cm}^{2}=55 \mathrm{~h} \mathrm{~cm}^{2}$

ar(trap. DCYX) ar(trap. ABYX) = 45h/55h = 9/11

⇒ ar(trap. DCYX) = 9/11 ar(trap. ABYX)