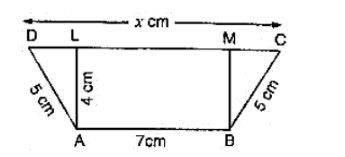
In figure, ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm, and distance between AB and DC is 4
Question:
In figure, ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm, and distance between AB and DC is 4 cm. Find the value of x and area of trapezium ABCD.
Solution:
Draw AL ⊥ DC, BM ⊥ DC then,
AL = BM = 4 cm and LM = 7 cm.
In Δ ADL, we have
$A D^{2}=A L^{2}+D L^{2}$
$\Rightarrow 25=16+\mathrm{DL}^{2}$
⇒ DL = 3 cm
Similarly,
$\mathrm{MC}=\sqrt{\mathrm{BC}^{2}-\mathrm{BM}^{2}}=\sqrt{25-16}=3 \mathrm{~cm}$
∴ x = CD = CM + ML + LD = (3 + 7 + 3) cm = 13 cm
$\operatorname{ar}(\operatorname{trap} \cdot \mathrm{ABCD})=1 / 2(\mathrm{AB}+\mathrm{CD}) \times \mathrm{AL}=1 / 2(7+13) \times 4 \mathrm{~cm}^{2}=40 \mathrm{~cm}^{2}$
