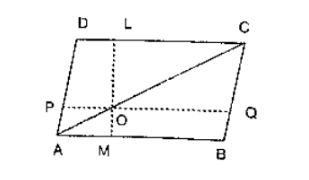
In figure, ABCD is a parallelogram. O is any point on AC. PQ ∥ AB and LM ∥ AD.

Since a diagonal of a parallelogram divides it into two triangles of equal area

Therefore, ar(ΔADC) = ar(ΔABC)

⇒ ar(ΔAPO) + ar(∥^gm DLOP) + ar(ΔOLC)

⇒ ar(ΔAOM) + ar(∥^gm BMOQ) + ar(ΔOQC)             ... (1)

Since AO and Oc are diagonals of parallelograms AMOP and OQCL respectively.

∴ ar(ΔAPO) = ar(ΔAMO)                .... (2)

And ar(ΔOLC) = ar(ΔOQC)              .... (3)

Subtracting 2 and 3 from 1, we get

ar(∥^gm DLOP) = ar(∥^gm BMOQ).