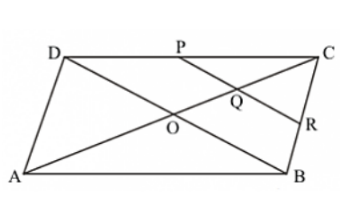
In Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = (1/2) AC.
Question:
In Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = (1/2) AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
Solution:
Join B and D.
Suppose AC and BD intersect at O.
Then OC = (1/2) AC
Now,
CQ = (1/4) AC
⇒ CQ = 1/2((1/2) AC)
= (1/2) OC
In ΔDCO, P and Q are mid points of DC and OC respectively.
∴ PQ ∥ DO
Also in ΔCOB, Q is the mid-point of OC and QR ∥ OB
Therefore, R is the mid-point of BC.