Question:
In figure, ABCD is a parallelogram and E is the mid-point of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.
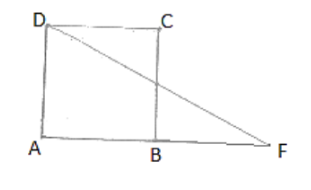
Solution:
In ΔBEF and ΔCED
∠BEF = ∠CED [Verified opposite angle]
BE = CE [Since, E is the mid-point of BC]
∠EBF = ∠ECD [Since, Alternate interior angles are equal]
∴ ΔBEF ≅ ΔCED [ASA congruence]
∴ BF = CD [CPCT]
AF = AB + AF
AF = AB + AB
AF = 2AB.
Hence proved.
