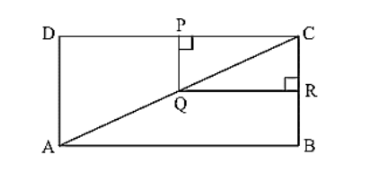
Question:
In figure, ABCD and PQRC are rectangles and Q is the mid-point of AC. Prove that
(i) DP = PC
(ii) PR = (1/2) AC
Solution:
(i) In ΔADC, Q is the mid-point of AC such that PQ∥AD
Therefore, P is the mid-point of DC.
⟹ DP = DC [Using mid-point theorem]
(ii) Similarly, R is the mid-point of BC
∴ PR = (1/2) BD
PR = (1/2) AC [Diagonal of rectangle are equal, BD = AC]
