Question:
In figure, ABCD and AEFD are two parallelograms. Prove that ar (APEA) = ar(AQFO).
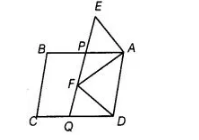
Solution:
Given, ABCD and AEFD are two parallelograms.
To prove ar (APEA) = ar (AQFD)
Proof In quadrilateral PQDA,
AP || DQ [since, in parallelogram ABCD, AB || CD ] and PQ || AD [since, in parallelogram AEFD, FE || AD]
Then, quadrilateral PQDA is a parallelogram.
Also, parallelogram PQDA and AEFD are on the same base AD and between the same parallels AD and EQ.
ar (parallelogram PQDA) = ar (parallelogram AEFD)
On subtracting ar (quadrilateral APFD) from both sides, we get
ar (parallelogram PQDA)- ar (quadrilateral APFD)
= ar (parallelogram AEFD) – ar (quadrilateral APFD) => ar (AQFD) = ar (APEA) Hence proved.
