In figure, AB and CD are two chords of a circle

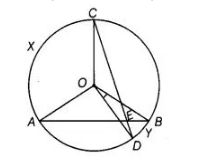
Given In a figure, two chords AB and CD intersecting each other at point E.

To prove $\quad \angle A E C=\frac{1}{2}$

[angle subtended by arc $C \times A$ at centre $+$ angle subtended by $\operatorname{arc} D Y B$ at the centre]

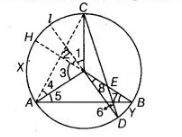
Construction Extend the line $D O$ and $B O$ at the points $l$ and $H$ on the circle. Also, join $A C$. Proof We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

$\therefore \quad \angle 1=2 \angle 6 \quad \ldots$ (i)

and $\quad \angle 3=2 \angle 7 \quad$...(ii)

$\begin{array}{lll}\text { In } \triangle A O C, & O C=O A & \text { [both are the radius of circle] }\end{array}$

$\angle O C A=\angle 4$ [angles opposite to equal sides are equal]

Also, $\angle A O C+\angle O C A+\angle 4=180^{\circ}$ 

[by angle sum property of triangle]

$\Rightarrow \quad \angle A O C+\angle 4+\angle 4=180^{\circ}$

$\Rightarrow \quad \angle A O C=180^{\circ}-2 \angle 4 \quad \ldots$ (iii)

Now, in $\triangle \mathrm{AEC}$, $\angle A E C+\angle E C A+\angle C A E=180^{\circ}$ 

[by angle property sum of a triangle]

$\Rightarrow \quad \angle A E C=180^{\circ}-(\angle E C A+\angle C A E)$

$\Rightarrow \quad \angle A E C=180^{\circ}-[(\angle E C O+\angle O C A)+\angle C A O+\angle O A E]$

$=180^{\circ}-(\angle 6+\angle 4+\angle 4+\angle 5)$

[in $\triangle O C D, \angle 6=\angle E C O$ angles opposite to equal sides are equal]

$=180^{\circ}-(2 \angle 4+\angle 5+\angle 6)$

$=180^{\circ}-\left(180^{\circ}-\angle A O C+\angle 7+\angle 6\right)$

[from Eq. (iii) and in $\triangle A O B, \angle 5=\angle 7$, as (angles opposite to equal sides are equal)]

$=\angle A O C-\frac{\angle 3}{2}-\frac{\angle 1}{2}$ [from Eqs. (i) and (ii)]

$=\angle A O C-\frac{\angle 1}{2}-\frac{\angle 2}{2}-\frac{\angle 3}{2}+\frac{\angle 2}{2}$  $\left[\right.$ adding and subtracting $\left.\frac{\angle 2}{2}\right]$

$=\angle A O C-\frac{1}{2}(\angle 1+\angle 2+\angle 3)+\frac{\angle 8}{2} \quad[\because \angle 2=\angle 8$ (vertically opposite angles) $]$

$=\angle A O C-\frac{\angle A O C}{2}+\frac{\angle D O B}{2}$

$\Rightarrow \quad \angle A E C=\frac{1}{2}(\angle A O C+\angle D O B)$

$=\frac{1}{2}$ [angle subtended by arc CXA at the centre $+$ angle subtended by arc DYB at the centre]