In Figure 5, ∆ABC is right angled at B,

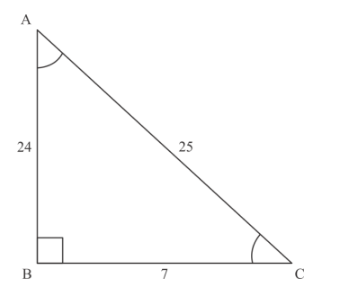
Solution:

It is given that is right angled at B, BC = 7 cm and AC − AB = 1 cm then we have to find the value of 

The following diagram is given

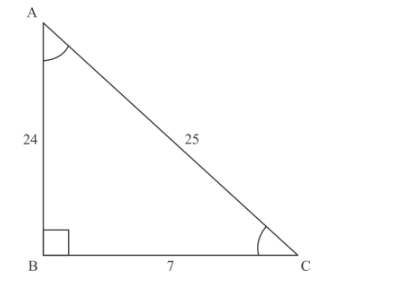
AC − AB = 1…… (1)

Now, apply the Pythagoras theorem in, we get

$A C^{2}=A B^{2}+B C^{2}$

$\Rightarrow \quad A C^{2}-A B^{2}=B C^{2}$

$\Rightarrow(A C-A B)(A C+A B)=7^{2}$

$\Rightarrow \quad A C+A B=9$..........(2)

Now add the equation (1) and (2), we get

$2 A C=50$

 

$\Rightarrow A C=25$

Put the value of in equation (2), we have

$25+A B=49$

$\Rightarrow A B=24$

Now,

$\cos A-\sin A=\frac{A B}{A C}-\frac{B C}{A C}$

$=\frac{24}{25}-\frac{7}{25}$

$=\frac{17}{25}$

Hence $\cos A-\sin A=\frac{17}{25}$