In Figure (1), O is the centre of the circle. If ∠OAB = 40° and ∠OCB = 30°, find ∠AOC.
Learn how to solve circle geometry problems involving central angles and angles subtended by the same arc using properties of radii and angle theorems, with step-by-step NCERT solutions for Class 10 Maths.
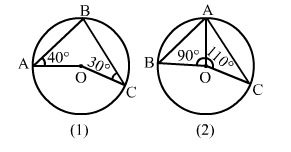
(i) In Figure (1), O is the centre of the circle. If ∠OAB = 40° and ∠OCB = 30°, find ∠AOC.
(ii) In Figure (2), A, B and C are three points on the circle with centre O such that ∠AOB = 90° and ∠AOC = 110°. Find ∠BAC.
(i) Join BO.
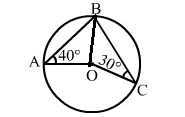
In ΔBOC, we have:
OC = OB (Radii of a circle)
⇒ ∠OBC = ∠OCB
∠OBC = 30° ...(i)
In ΔBOA, we have:
OB = OA (Radii of a circle)
⇒∠OBA = ∠OAB [∵ ∠OAB = 40°]
⇒∠OBA = 40° ...(ii)
Now, we have:
∠ABC = ∠OBC + ∠OBA
= 30° + 40° [From (i) and (ii)]
∴ ∠ABC = 70°
The angle subtended by an arc of a circle at the centre is double the angle subtended by the arc at any point on the circumference.
i.e., ∠AOC = 2∠ABC
= (2 × 70°) = 140°
(ii)
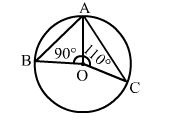
Here, $\angle B O C=\left\{360^{\circ}-\left(90^{\circ}+110^{\circ}\right)\right\}$
$=\left(360^{\circ}-200^{\circ}\right)=160^{\circ}$
We know that ∠BOC = 2∠BAC
$\Rightarrow \angle B A C=\frac{\angle B O C}{2}=\left(\frac{160^{\circ}}{2}\right)=80^{\circ}$
Hence, ∠BAC = 80°
Frequently Asked Questions
Find answers to common questions.
What is ∠AOC when ∠OAB = 40° and ∠OCB = 30°?
∠AOC = 140°. Using isosceles triangles OAB and OCB (radii are equal), we get ∠OBA = 40° and ∠OBC = 30°. So ∠ABC = 70°. By the central angle theorem, ∠AOC = 2 × 70° = 140°. This result comes directly from NCERT Class 9 Maths Chapter 10, Exercise 10.5.
Why is the angle at the centre double the angle at the circumference?
This is the Central Angle Theorem, a fundamental result in Euclidean geometry. The proof uses the exterior angle property of triangles: when you draw a radius to the inscribed angle's vertex, you form two isosceles triangles. The exterior angle of each triangle equals twice the base angle, and when combined, this gives the central angle as exactly twice the inscribed angle.
Can ∠ABC be found without joining BO?
Not directly with this approach. The construction of BO is essential because it splits ∠ABC into ∠OBA and ∠OBC, each of which can be found using the isosceles triangle property. Without BO, there is no clear link between the two given angles ∠OAB and ∠OCB.
What does the central angle theorem say in simple terms?
.
In simple terms: if you stand at the centre of a circle and look at an arc, the angle you see is exactly twice the angle someone standing anywhere on the opposite arc would see looking at the same arc. The centre always sees double what the circumference sees — for any arc, any position on the remaining circumference.
Is the central angle theorem relevant for JEE Main?
Yes. While JEE Main does not test Class 9 content directly, circle geometry — including arc-angle relationships — appears in coordinate geometry and complex number problems. Students who have strong intuition about angle relationships from Class 9 find JEE circle problems significantly easier. The IIT Bombay faculty at eSaral build this foundation deliberately in their Class 9 courses so students carry it forward to JEE preparation.