In Fig. 8, and ΔDBC are on the same base BC and on opposite sides of BC ad Q is the point of intersection of AD and BC.
Prove that $\frac{\operatorname{area}(\Delta A B C)}{\operatorname{area}(\Delta D B C)}=\frac{A O}{D O}$
We have given the diagram in which
We have to prove that $\frac{\text { Area of } \triangle A B C}{\text { Area of } \triangle D B C}=\frac{A O}{D O}$
Firstly, we draw a line from A perpendicular to line BC and after that we draw a line from D perpendicular to BC.
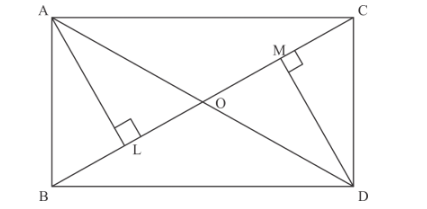
From the above figure we can easily see that the![]() and
and ![]() are similar
are similar
Therefore by the properties of similar triangle, we have
$\frac{A L}{D M}=\frac{A O}{D O} \ldots \ldots$(1)
Now,
$\frac{\text { Area of } \triangle A B C}{\text { Area of } \triangle D B C}=\frac{\frac{1}{2} B C \cdot A L}{\frac{1}{2} B C \cdot D M}$
$=\frac{A L}{D M}$
From equation (1), we get
$\frac{\text { Area of } \triangle A B C}{\text { Area of } \triangle D B C}=\frac{A O}{D O}$
Hence proved.
