In Fig. 7, AB ⊥ BC, FG ⊥ BC and DE ⊥ AC.

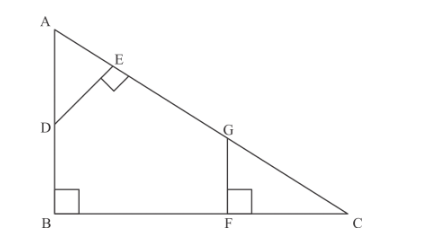
Solution:

In the given figure, we have

$A B \perp B C$

$F G \perp B C$, and

$D E \perp A C$

Then we have to prove that 

The following diagram is given

In, we have

$\angle A+\angle D=90^{\circ}$.......(1)

In $\triangle A B C$, we have

$\angle A+\angle C=90^{\circ} \ldots \ldots(2)$

From equation (1) and equation (2), we have

$\angle A+\angle C=\angle A+\angle D$

$\Rightarrow \quad \angle C=\angle D$

Similarly, we have

$\angle A=\angle G$

Since $\triangle A D E$ and $\triangle G C F$ are equiangular, therefore $\triangle A D E \sim \triangle G C F$