In Fig. 6, AD ⊥ BC and BD =

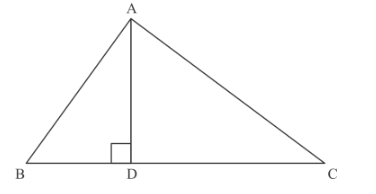
In the given figure, we have

$A D \perp B C$ and $B D=\frac{1}{3} C D$, then we have to prove $2 C A^{2}=2 A B^{2}+B C^{2}$

The following given diagram is

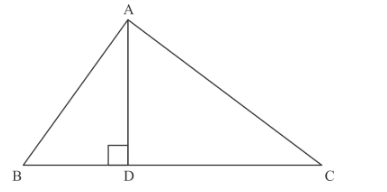
Now, suppose the value of BD is x, then

$B D=\frac{1}{3} C D$

$\Rightarrow \quad x=\frac{1}{3} C D$

$\Rightarrow C D=3 x$

$B C=B D+C D$

$=x+3 x$

$=4 x$

In triangle ADC, we have

$C A^{2}=C D^{2}+A D^{2} \ldots \ldots(1)$

And in triangle ADB, we have

$A B^{2}=B D^{2}+A D^{2}$

$\Rightarrow A D^{2}=A B^{2}-B D^{2} \ldots \ldots(2)$

Now add the equation (1) and equation (2), we get

$C A^{2}+A D^{2}=C D^{2}+A B^{2}-B D^{2}+\mathrm{AD}^{2}$

$\Rightarrow \quad C A^{2}=A B^{2}+C D^{2}-B D^{2}$.......(3)

Now we are putting the values of BD and CD, we get

$C A^{2}=A B^{2}+(3 x)^{2}-x^{2}$

$\Rightarrow \quad C A^{2}=A B^{2}+8 x^{2}$

$\Rightarrow \quad C A^{2}=A B^{2}+\frac{1}{2} \times(4 x)^{2}$

$\Rightarrow 2 C A^{2}=2 A B^{2}+B C^{2}$

Hence proved.