In Fig. 4, OABC is a square inscribed in a quadrant OPBQ.

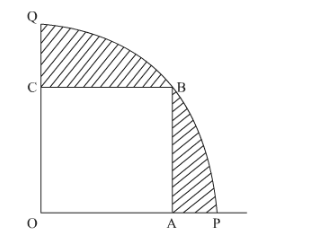
It is given that OABC is a square in the quadrant OPBQ.OA is 20 cm.

We have to find the area of the shaded region.

OABC is a square , therefore sides of the OABC must be equal

Hence OA, AB, BC, OC = 20 cm.

Join the points O and B to form a line segment OB.

Since OB is the diagonal of OABC, is a right angled triangle.

Applying Pythagoras Theorem in 

It can be seen from the figure that $Q$ uadrant $O P B Q$ is $\frac{1}{4}$ of a circle with radius $O B(r)$

Therefore area of $O P B Q=\frac{1}{4} \pi r^{2}$

Now, area of the shaded region $=$ area of $O P B Q$-area of $O A B C$

$=\frac{1}{4} \pi r^{2}-s^{2} \quad$ (area of a square with side $s=s^{2}$ )

$=\frac{1}{4} \times 3.14 \times(20 \sqrt{2})^{2}-20^{2}$

$=\frac{1}{4} \times 3.14 \times 800-400$

$=628-400$

$=228$

Area of the shaded region $=228 \mathrm{~cm}^{2}$