In Fig. 3, two tangents PQ are PR are drawn to a

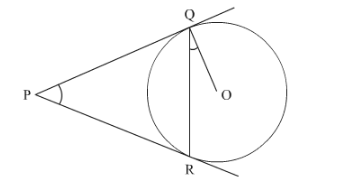
Given a figure as shown. We have to prove that 

Join OR

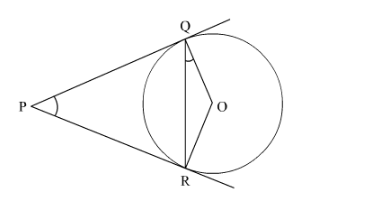
We know that sum of opposite angles of a cyclic quadrilateral 

Therefore in quadrilateral PQOR,

$\angle Q O R=180^{\circ}-\angle Q P R$

In $\triangle O Q R$

$O Q=O R$ [Since $O Q, O R$ are radii of the circle]

Therefore $\triangle O Q R$ is an isosceles triangle.

Hence [Angles opposite to equal side of isosceles triangle]

Now, $\angle O Q R=\frac{1}{2}\left(180^{\circ}-\angle Q O R\right)$ [since, $\angle O Q R=\angle O R Q$ ]

$\angle O Q R=\frac{1}{2}\left(180^{\circ}-\left(180^{\circ}-\angle Q P R\right)\right)$ [From (1)]

$\angle O Q R=\frac{1}{2}(\angle Q P R)$

$\angle Q P R=2 \angle O Q R$

Hence proved.