In Fig. 2, a circle of radius 7 cm is inscribed in a square.

It is given that a circle of radius 7 cm is inscribed in a square

We have to find the area of shaded region shown in figure

We are given the following figure

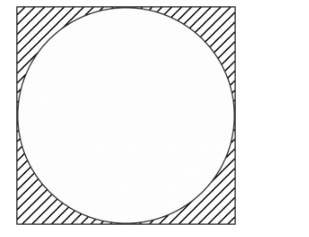
Let the side of the square = a cm

Since the circle in inscribed in the square

Diameter of the circle = a cm

Radius of circle $=\frac{a}{2} \mathrm{~cm}$

Given that radius of circle = 7 cm

Therefore

$\frac{a}{2}=7 \mathrm{~cm}$

$a=14 \mathrm{~cm}$

Area of square $=a^{2}$

$=14^{2} \mathrm{~cm}^{2}$

$=196 \mathrm{~cm}^{2}$

Area of circle $=\pi$ (radius) $^{2}$

$=\pi \times 7^{2} \mathrm{~cm}^{2}$

$=49 \times \frac{22}{7} \mathrm{~cm}^{2}$

$=154 \mathrm{~cm}^{2}$

Area of shaded region $=$ Area of square $-$ Area of circle

$=196-154 \mathrm{~cm}^{2}$

$=42 \mathrm{~cm}^{2}$