In below fig. OP, OQ, OR and OS are four rays. Prove that: ∠POQ + ∠QOR + ∠SOR + ∠POS = 360°

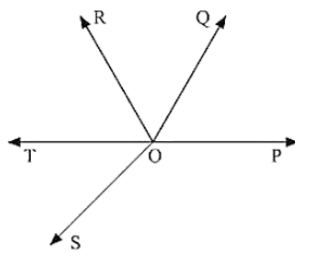
Solution:

Given that

OP, OQ, OR and OS are four rays

You need to produce any of the ray OP, OQ, OR and OS backwards to a point in the figure.

Let us produce ray OQ backwards to a point T

So that TOQ is a line

Ray OP stands on the TOQ

Since ∠TOP, ∠POQ is a linear pair

∠TOP + ∠POQ = 180° ... (1)

Similarly,

Ray OS stands on the line TOQ

∠TOS + ∠SOQ = 180° ... (2)

But ∠SOQ = ∠SOR + ∠QOR  ... (3)

So, eqn (2) becomes

∠TOS + ∠SOR + ∠OQR = 180°

Now, adding (1) and (3) you get ∠TOP + ∠POQ + ∠TOS + ∠SOR + ∠QOR = 360° ... (4)

∠TOP + ∠TOS = ∠POS

Eqn: (4) becomes

∠POQ + ∠QOR + ∠SOR + ∠POS = 360°