In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:<br/><br/>(i) $\mathrm{OB}=\mathrm{OC}$<br/><br/>(ii) $\mathrm{AO}$ bisects $\angle \mathrm{A}$

Solution:



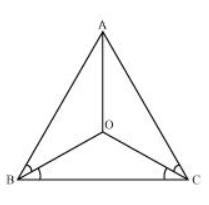
(i) It is given that in triangle $A B C, A B=A C$

$\Rightarrow \angle A C B=\angle A B C$ (Angles opposite to equal sides of a triangle are equal)

$\Rightarrow \frac{1}{2} \angle \mathrm{ACB}=\frac{1}{2} \angle \mathrm{ABC}$

$\Rightarrow \angle \mathrm{OCB}=\angle \mathrm{OBC}$

$\Rightarrow O B=O C$ (Sides opposite to equal angles of a triangle are also equal)

(ii) In $\triangle \mathrm{OAB}$ and $\triangle \mathrm{OAC}$,

$\mathrm{AO}=\mathrm{AO}$ (Common)

$\mathrm{AB}=\mathrm{AC}$ (Given)

OB = OC (Proved above)

Therefore, $\triangle \mathrm{OAB} \cong \triangle \mathrm{OAC}$ (By SSS congruence rule)

$\Rightarrow \angle B A O=\angle C A O(C P C T)$

$\Rightarrow \mathrm{AO}$ bisects $\angle \mathrm{A}$