In an isosceles triangle ABC, AB = AC = 25 cm,

We know that altitude that is a perpendicular drawn on the unequal side of the isosceles triangle bisects that side.

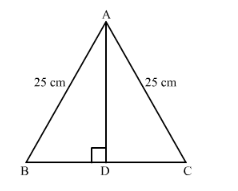
Therefore, BD = DC = 7 cm.

Let us use the Pythagoras theorem in right angled triangle ADB we get,

$A B^{2}=A D^{2}+B D^{2}$

Substituting the values we get,

$25^{2}=A D^{2}+7^{2}$

$\therefore 625=A D^{2}+49$

Subtracting 49 from both the sides we get,

$625-49=A D^{2}$

$\therefore A D^{2}=576$

Let us take the square root we get,

AD = 24 cm

Therefore, the altitude of the isosceles triangle is .