In $\triangle A B C, D$ is the mid-point of $A B$ and $P$ is any point on $B C$. If $C Q \| P D$ meets $A B$ in $Q$ (shown in figure), then prove that ar $(\triangle B P Q)=1 / 2 \operatorname{ar}(\triangle A B C)$.
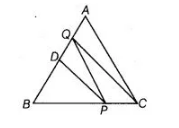
Given in $\triangle A B C, D$ is the mid-point of $A B$ and $P$ is any point on $B C$.
$C Q \| P D$ means $A B$ in $Q$.
To prove $\operatorname{ar}(\triangle B P Q)=\frac{1}{2} \operatorname{ar}(\triangle A B C)$
Construction Join $P Q$ and $C D$.
Proof Since, $D$ is the mid-point of $A B$. So $C D$ is the median of $\triangle A B C$.
We know that, a median of a triangle divides it into two triangles of equal areas.
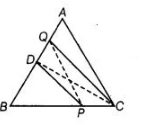
$\therefore \quad a r(\Delta B C D)=\frac{1}{2} \operatorname{ar}(\triangle A B C)$
$\Rightarrow \quad \operatorname{ar}(\Delta B P D)+\operatorname{ar}(\Delta D P C)=\frac{1}{2} \operatorname{ar}(\Delta A B C)$ $\ldots$ (i)
Now, $\triangle D P Q$ and $\triangle D P C$ are on the same base $D P$ and between the same parallel lines $D P$ and $C Q$.
So, $\operatorname{ar}(\triangle D P Q)=\operatorname{ar}(\triangle D P C)$ ....(ii)
On putting the value from Eq. (ii) in Eq. (i), we get
$\operatorname{ar}(\Delta B P D)+\operatorname{ar}(\triangle D P Q)=\frac{1}{2} \operatorname{ar}(\triangle A B C)$
$\Rightarrow$ $\operatorname{ar}(\Delta B P Q)=\frac{1}{2} \operatorname{ar}(\triangle A B C)$
Hence proved.
