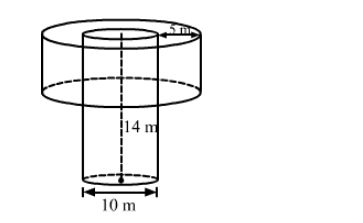
In a village, a well with 10 m inside diameter, is dug 14 m deep.

We have,

Radius of well, $R=\frac{10}{2}=5 \mathrm{~m}$,

Depth of the well, $H=14 \mathrm{~m}$ and

Width of the embankment $=5 \mathrm{~m}$,

Also, the outer radius of the embankment, $r=R+5=5+5=10 \mathrm{~m}$

And, the inner radius of the embankment $=R=5 \mathrm{~m}$

Let the height of the embankment be $h$.

Now,

Volume of the embankment = Volume of the earth taken out

$\Rightarrow$ Volume of the embankment $=$ Volume of the well

$\Rightarrow\left(\pi r^{2}-\pi R^{2}\right) h=\pi R^{2} H$

$\Rightarrow \pi\left(r^{2}-R^{2}\right) h=\pi R^{2} H$

$\Rightarrow\left(r^{2}-R^{2}\right) h=R^{2} H$

$\Rightarrow\left(10^{2}-5^{2}\right) h=5 \times 5 \times 14$

$\Rightarrow(100-25) h=25 \times 14$

$\Rightarrow 75 h=25 \times 14$

$\Rightarrow h=\frac{25 \times 14}{75}$

$\therefore h=\frac{14}{3} \mathrm{~m}$

So, the height of the embankment is $\frac{14}{3} \mathrm{~m}$.

Value: We must lanour hard to make maximum use of the available resources.

Disclaimer: The answer provided in the textbook is incorrect. It has been corrected above.