In a triangle ABC with ∠C

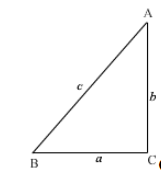
${ }^{\mathrm{C}}$ Given in Triangel $A B C$,

$\angle C=\pi / 2$

$\Rightarrow \angle A+\angle B=\pi / 2 \quad(\because \angle A+\angle B+\angle C=\pi$ sum of angle of triangle is $\pi)$

Equation with roots $\tan A$ and $\tan B$ is of the form,

$(x-\tan A)(x-\tan B)=0$

i. e. $x^{2}=(\tan A+\tan B) x+\tan A \tan B=0$

Since $\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B}$

i. e. $\tan (\pi / 2)=\frac{\tan A+\tan B}{1-\tan A \tan B}$

i. e. $\infty=\frac{\tan A+\tan B}{1-\tan A \tan B}$

i. e. $1-\tan A \tan B=0$

i.e. $\tan A \tan B=1$

$\therefore$ equation reduces to $x^{2}-(\tan A+\tan B) x+1=0$

Let us denote side $A B$ by $c$

$A C$ by $b$

$B C$ by a

$\tan A=\frac{a}{b}, \tan B=\frac{b}{a}$

$\therefore x^{2}-\left(\frac{a}{b}+\frac{b}{a}\right) x+1=0$

i. e. $x^{2}-\frac{\left(a^{2}+b^{2}\right) x}{a b}+1=0 \quad\left[\right.$ By pythagoras them, $\left.a^{2}+b^{2}=c^{2}\right]$

i. e. $x^{2}-\frac{c^{2} x}{a b}+1=0$

i. e. $a b x^{2}-c^{2} x+1=0$

$\therefore$ equation with roots $\tan A$ and $\tan B$ is of the form $a b x^{2}-c^{2} x+1=0$.