Question:
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
Solution:
Let A, B, and C be the set of people who like product A, product B, and product C respectively.
Accordingly, $n(\mathrm{~A})=21, n(\mathrm{~B})=26, n(\mathrm{C})=29, n(\mathrm{~A} \cap \mathrm{B})=14, n(\mathrm{C} \cap \mathrm{A})=12$
$n(B \cap C)=14, n(A \cap B \cap C)=8$
The Venn diagram for the given problem can be drawn as
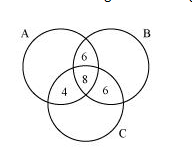
It can be seen that number of people who like product C only is
$\{29-(4+8+6)\}=11$
