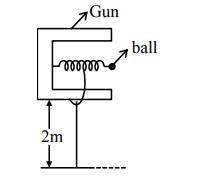
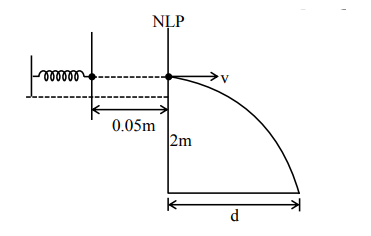
In a spring gun having spring constant $100 \mathrm{~N} / \mathrm{m}$ a small ball 'B' of mass $100 \mathrm{~g}$ is put in its barrel (as shown in figure) by compressing the spring through $0.05 \mathrm{~m}$. There should be a box placed at a distance 'd' on the ground so that the ball falls in it. If the ball leaves the gun horizontally at a height of $2 \mathrm{~m}$ above the ground. The value of $d$ is_______m.
$\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)$
$\frac{1}{2} \mathrm{kx}^{2}=\frac{1}{2} \mathrm{mv}^{2}$
$\mathrm{Kx}^{2}=\mathrm{mv} \mathrm{v}^{2}$
$\mathrm{v}=\mathrm{x} \sqrt{\frac{\mathrm{k}}{\mathrm{m}}}=0.05 \sqrt{\frac{100}{0.1}}=0.05 \times 10 \sqrt{10}$
$\mathrm{v}=0.5 \sqrt{10}$
From $\mathrm{h}=\frac{1}{2} \mathrm{gt}^{2}$
$t=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 2}{10}}=\frac{2}{\sqrt{10}}$
$\therefore \mathrm{d}=\mathrm{vt}=0.5 \sqrt{10} \times \frac{2}{\sqrt{10}}=1 \mathrm{~m}$
