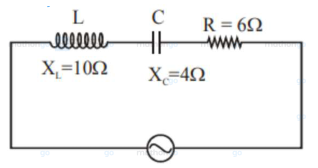
In a series LCR circuit, the inductive reactance $\left(X_{L}\right)$ is $10 \Omega$ and the
capacitive reactance $\left(\mathrm{X}_{\mathrm{C}}\right)$ is $4 \Omega$. The resistance $(\mathrm{R})$ in the circuit is $6 \Omega$.
The power factor of the circuit is:
Correct Option: 3,
(3)
We know that power factor is $\cos \phi$,
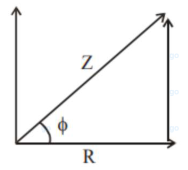
$\cos \phi=\frac{\mathrm{R}}{\mathrm{Z}} \ldots(1)$
$\mathrm{Z}=\sqrt{\mathrm{R}^{2}+\left(\mathrm{X}_{\mathrm{L}}-\mathrm{X}_{\mathrm{C}}\right)^{2}}$
$(\omega L-1 / \omega C)$
$\Rightarrow Z=\sqrt{6^{2}+(10-4)^{2}}$
$\Rightarrow \mathrm{Z}=6 \sqrt{2} \mid \cos \phi=\frac{6}{6 \sqrt{2}}$
$\cos \phi=\frac{1}{\sqrt{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.