In a meeting, 70% of the members favour and 30% oppose a certain proposal.

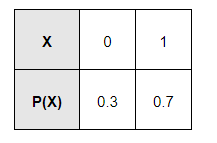
It is given that $P(X=0)=30 \%=\frac{30}{100}=0.3$

$\mathrm{P}(\mathrm{X}=1)=70 \%=\frac{70}{100}=0.7$

Therefore, the probability distribution is as follows.

Then, $E(X)=\sum X_{i} P\left(X_{i}\right)$

$=0 \times 0.3+1 \times 0.7$

$=0.7$

$\mathrm{E}\left(\mathrm{X}^{2}\right)=\sum \mathrm{X}_{\gamma}^{2} \mathrm{P}\left(\mathrm{X}_{i}\right)$

$=0^{2} \times 0.3+(1)^{2} \times 0.7$

$=0.7$

It is known that, $\operatorname{Var}(\mathrm{X})=\mathrm{E}\left(\mathrm{X}^{2}\right)-[\mathrm{E}(\mathrm{X})]^{2}$

$=0.7-(0.7)^{2}$

$=0.7-0.49$

$=0.21$